To Find the Refractive Index of a Liquid by Using Convex Lens and Plane Mirror

Table of Contents

Aim/Aim of Experiment

To find the Refractive Index of a Liquid by using Convex
Lens and Plane Mirror.

Apparatus/Material Required

Convex lens
A Plane mirror
An optical Needle
The clean transparent Liquid in beaker
An Iron stand with base and clamp arrangement
Pump line
A plane glass slab
A spherometer
A half meter scale

Theory

Let us consider f₁ and f₂ are the focal lengths of glass convex lens and liquid lens respectively, Let F be the focal length of their combination then,

1/F=1/f₁+1/f₂ or 1/f₂=1/F-1/f₁

The Liquid lens formed is a plano-concave lens with R₁=R, and R₂=∞.

So, from lens maker’s formula,

1/f₂=(n-1)[1/R₁-1/R₂]

we have 1/f₂=(n-1)/R,

If R be the radius of curvature of the convex lens which is in contact with the liquid then the refractive index of the liquid is, n=1+R/f₂.

Where n is the refractive index of the liquid and by putting the value of f₂ then n can be calculated.

Diagram

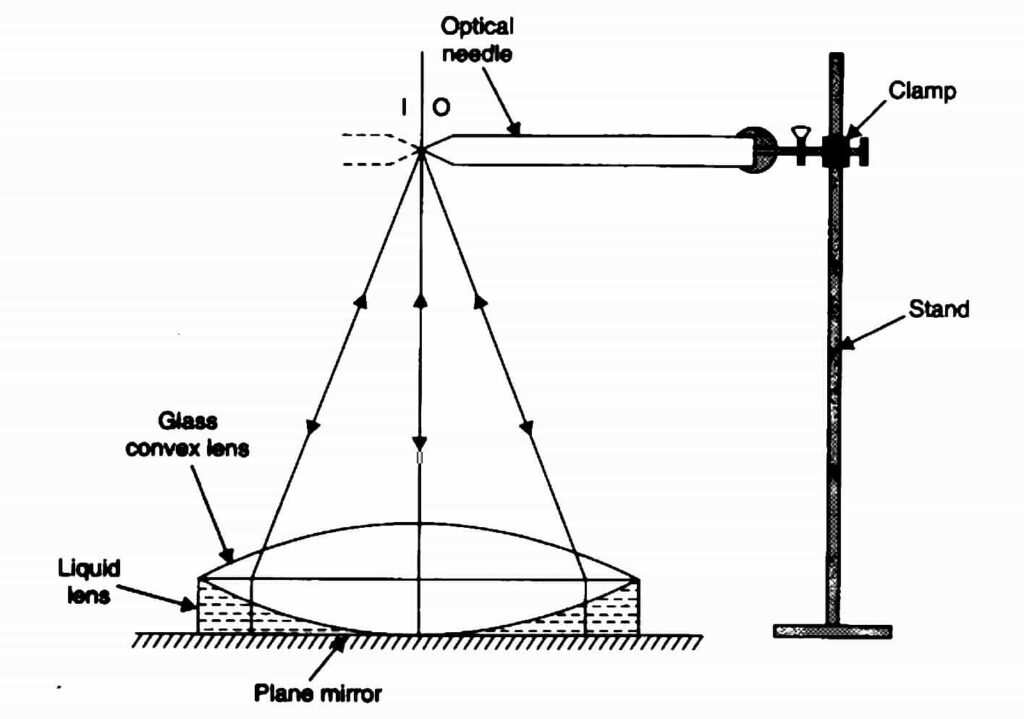
Refractive Index of a Liquid by using Convex lens and Plane mirror

Procedure

For the Focal length of Canvex lens:

Take a convex lens and find its rough focal length.
Place the plane mirror horizontally on the base of the iron stand with its reflecting surface upward and place the convex lens on the plane mirror.
Tight the screw of optical needle in the clamp of the stand and hold it horizontally above the lens at distance equal to its rough focal length.
For the tip of the needle appears touching the tip of its image, bring the tip of the needle at the vertical principal axis of the lens.
To remove parallax between tips of the needle and its image, move the needle up and down, so that image and object will be the same size.
Measure the distance between tip and upper surface of the lens by using a plumb line and half metre scale, also measure the distance between tip and the surface of its plane mirror.

For the Focal length of the combination:

Firstly remove the lens and take few drops of the given transparent liquid on the plane mirror.
Now place the convex lens over the liquid with its same face in cantact with the liquid above as before.
Repeat the Steps 5 and 6 of the above.
Record your observations.

For the radius of curvature of convex lens surface:

A plano-concave lens formed between the convex lens and the plane mirror so radius will be R₁=R, and R₂ =∞.
From lens maker’s formula 1/f2=(n-1)[1/R₁-1/R₂ becomes 1/f₂=(n-1)/R.
Now the radius of curvature of the Canvex lens can be calculated by the formula R=(n-1)f₂, where n is the refractive index of the liquid.

Observations

1. The rough focal length of the convex lens = 35 cm.

2. Table for distance of needle tip from Lens and Mirror:

Arrangement	Distance of needle tip from lens surface x₁ (cm)	Distance of needle tip from plane mirror x₂ (cm)	Distance of needle tip Mean [x=(x₁+x₂)/2]	Focal Length x (cm)
(1)	(2a)	(2b)	(2c)	(3)
Without Liquid	34.5	35	34.75	f₁=34.75
With Liquid	51.5	49	50.25	F=50.25

3. The Radius of curvature of the Convex lens surface = 70 cm.

Calculations

1. Calculation for the focal length of liquid lens:

1/f₂=1/F-1/f₁,

putting the value of F and f₁,

So, 1/f₂ = 1/34.75-1/50.25

=0.02878-0.01990

1/f₂ = 0.00888,

Hence, f₂=1/0.00888 = 112.612.

2. Calculation for the refractive index of the liquid:

n=1+R/f₂,

putting the value of R and F₂,

n=[1+(70/112.612)]

= 1+0.6216

Hence, n = 1.6216.

Result

The refractive index of the liquid is, n=1.6216.

Precautions

The liquid taken should be clean and transperant.
The layer of liquid not be thick, so only a few drops of liquid should be taken.
The parallax should be removed tip to tip.

Sources of Error

The taken liquid not be quite transperant.
The parallax may not be fully removed.

Class 12 Physics Practicals: